課題7-1
-2π < x < 2πの範囲で y = sin(2x), y = cos(x), y = tan(x), y = exp(0.2x) の関数を重ねてグラフに表示せよ。表示した結果をPNGファイルに書き出し、TACTの添付ファイルとして提出せよ。課題7-2
温度 T [K] の黒体が放射する単位波⻑あたりの放射強度(intensity) I [J/(m 2 s str m)]は、波⻑[m]をλとすると以下の式で表される。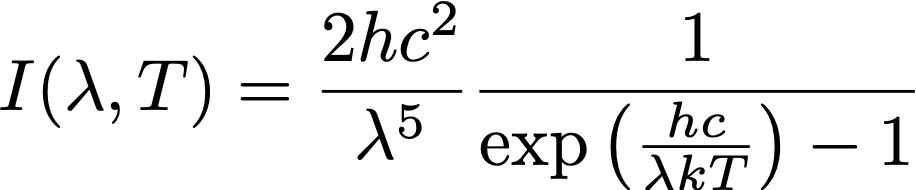
7-2-1 関数定義
Python上で上式を x = λ, y = Tとし I(x,y) の形で関数を定義し、その式をTACTの入力欄に解答せよ。ただし、c (光速), h (プランク定数), k (ボルツマン定数) を次のように定義する。Python上でのc, h, kの定義式も含めて解答せよ。c (m/s) = 2.99792458e8
h (J s) = 6.626068e-34
k (J/K) = 1.3806504e-23
7-2-2 2次元プロット
T = 60000 K, 6000 K, 600 Kの時の放射強度スペクトルを表示し、そのPNGファイルを添付せよ。縦軸、横軸共に対数表示、横軸は波⻑(1nmから1cm)、縦軸は放射強度(見易いように調整せよ)とする(ax.set_xscale("log")で横軸が対数表示になるので、縦軸も同様にせよ。その他、軸の範囲の調整なども講義資料を参考にせよ)。またそれぞれの温度の時に放射強度が最大になる波⻑を有効数字一桁でグラフから読み取り、その値をTACTの入力欄に解答せよ. 各軸のラベルもきちんと表示しておくこと。ヒント: 波⻑を1 nmから1 cmまでを100点ほどで表そうと、
x=np.linspace(1e-9,1e-2,100) などとした場合、サンプリング間隔が広すぎて横軸を対数表示にした際にうまく描画できない。
講義で習ったようにx=np.logspace(-9,-2,100) として対数表示に適したサンプリングをしよう。