課題10-1
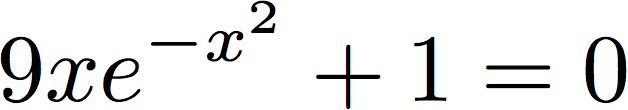は2つの解があるが、そのうちの大きい方を求めたい。
(Pythonのグラフ描画により解をあらかじめ見積もっておくと見通しが良い。)
そのプログラムを、
a. Newton-Raphson法
b. 2分法
のそれぞれの方法を用いて作成せよ。 そして、以下について調べよ。
- Newton-Raphson法を用いたプログラムで初期の推測値をx=1とした場合、正しい解は求められるか？ 求められない場合、なぜ求められないか考察し、どのような初期推測値を設定すると解が求められるかを調べよ。
- 適切な解の範囲を設定した上で、2分法を用いて解を求めよ。この時、初期に設定した解の範囲と、反復回数を答えよ。
Newton-Raphson法および二分法それぞれのソースコードと、上記1,2を調べた考察結果をTACTにより提出せよ。
課題10-2
平均μ、標準偏差σ(分散σ2)を持つ、正規分布関数f(x)は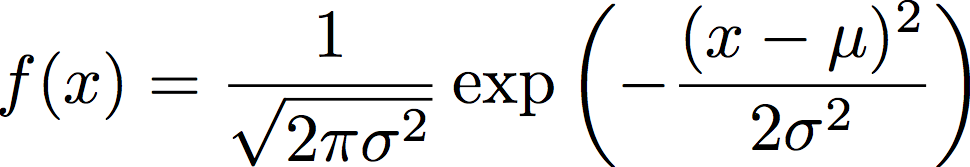
のように表される。x=-∞からx=∞までf(x)を積分すると1となるよう規格化されている。
受講生100名の授業で100点満点の試験を行ったところ、得点分布は、平均が75点、 標準偏差が10点の正規分布に従っていたという。その場合
- 得点が65点から85点まで(偏差値が40から60、すなわち平均値から±1σに対応)の人数 (小数点以下は四捨五入せよ)。
- 得点が90点以上(偏差値が65以上に対応)の人数。 但し積分の上限を満点の100点として良い。
課題10-3 追加問題(必答では無いが取り組んだ場合は加点)
適当な関数を数値積分することによって、円周率πを求めよ。 台形公式およびシンプソンの公式の両方を用いて定積分を行い、結果を比較せよ。課題の提出には、ソースプログラムの他に、それぞれの公式を用いた場合の積分値と、 実際のπの値を比較したものTACT の入力欄に記せ。
(参考) 講義資料の台形公式とシンプソン公式の章のサンプルプルグラム
(ヒント) πの求め方が分からない人は円の面積を使用すれば良い。 もちろん他の方法でも良い。